Sudoku

Sudoku is an easy to learn logic-based number placement puzzle. The word Sudoku is short for Su-ji wa dokushin ni kagiru which means "the numbers must be single".

The roots of the Sudoku puzzle are in the Switzerland. Leonhard Euler created "carré latin" in the 18st century which is similar to a sudoku puzzle but without the additional constraint on the contents of individual regions. The first real Sudoku was published in 1979 and was invented by Howard Garns, an American architect.

The real world wide popularity started in Japan in 1986 after it was published and given the name Sudoku by Nikoli.

Rules and Terms

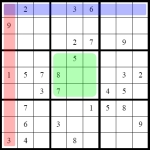A Sudoku puzzle consists of 81 cells which are divided into nine cols, rows and regions. The task is now to place the numbers from 1 to 9 into the empty cells in such a way that in every row, column and 3×3 region each number appears only once.

A Sudokus has at least 17 givens numbers but normally there are 22 to 30.

Mathematics

A Sudoku is a logic-based and not a math-based puzzle. It is possible to make und solve a Sudoku puzzle with letters or even some symbols.

A little interesting point is that there are 6.670.903.752.021.072.936.960 possible Sudoku puzzles. So we can play umpteen Sudokus a day and there will still be new ones.

How to solve a Sudoku (Example)

Firstly this is a guide for absolute beginners. I know there are better and/or more elegant ways to solve a Sudoku but I only tried to write a little overview and not the ultimate Sudoku guide.

Step 1
	Here in step 1 we have an example Sudoku. It has only the level easy but for this example it will be enough. A possible place to begin such a puzzle is to search for a number which appears most frequently.
Step 2
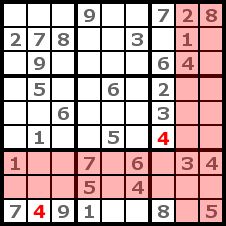	We will try the 4 first. We look now for regions without a 4 and try to place the 4 by a process of elimination. For this purpose we identify which cols and rows contain a 4 because in the cells of this rows and cols we can't put the 4. If only one possible place left in a region we place the 4 there. That's how we got the two 4 in the picture. This strategy is named cross-hatching.
Step 3
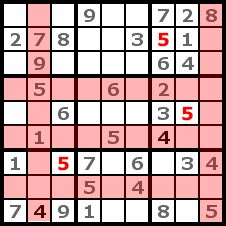	We repeat the cross-hatching with the number 5. This is even more effective then with the number 4 because we can place three 5.
Step 4
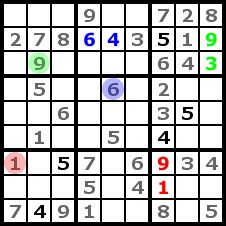	In this step we can now complete the rows, cols and regions with only two empty cells left. This is easy to do because for one cell of each two cell groups is only one possible number left. To make this easier to understand I highlighted it with colours. Such a step like this will make cross-hatching and counting simpler in the next steps.
Step 5
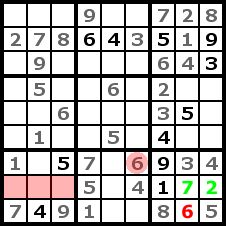	At the lower left region we can't determine the exact position of the number 6, but we know into which row we have to put it (the three red cells). Thereby we can now place the 6 in the lower right region. Then we can get the 7 and 2 like in step 4.
Step 6
	Now we can't find any more numbers by cross-hatching. That's why we try it with counting. We count regions, rows, and columns to identify missing numerals for a cell. If we found a cell with only one possible number left after counting we place it into the cell. It is helpful to write little numbers into a cell to help memorise the findings of the counting. By this we got six numbers in this step.
Step 7
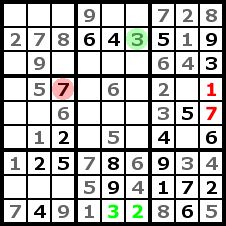	Analogue to step 4 we can complete now a row and a column of our puzzle.
Step 8
	We can find a few numbers in this step by counting like in step 6.
Step 9
	And now the solutions of the sudoku puzzle. We skipped a few steps because there wasn't any knew in them but only repetitions of the other steps.